•驗證: 與DFMEA結合使用,評估風險程度和驗證程序控制機制,防止問題再現;可靠性模型;設計參數預測
蒙特卡羅方法分子類比計算的步驟
使用蒙特·卡羅方法進行分子類比計算是按照以下步驟進行的:
1. 使用亂數發生器產生一個隨機的分子構型。
2. 對此分子構型的其中粒子座標做無規則的改變,產生一個新的分子構型。
3. 計算新的分子構型的能量。
4. 比較新的分子構型于改變前的分子構型的能量變化,判斷是否接受該構型。
若新的分子構型能量低於原分子構型的能量,則接受新的構型,使用這個構型重複再做下一次反覆運算。
若新的分子構型能量高於原分子構型的能量,則計算玻爾茲曼因數,並產生一個亂數。
若這個亂數大於所計算出的玻爾茲曼因數,則放棄這個構型,重新計算。
若這個亂數小於所計算出的玻爾茲曼因數,則接受這個構型,使用這個構型重複再做下一次反覆運算。
5. 如此進行反覆運算計算,直至最後搜索出低於所給能量條件的分子構型結束。
蒙特卡羅模型的運用
蒙特卡羅方法有很強的適應性,問題的幾何形狀的複雜性對它的影響不大。該方法的收斂性是指概率意義下的收斂,因此問題維數的增加不會影響它的收斂速度,而且存貯單元也很省,這些是用該方法處理大型複雜問題時的優勢。因此,隨著電子電腦的發展和科學技術問題的日趨複雜,蒙特卡羅方法的應用也越來越廣泛。它不僅較好地解決了多重積分計算、微分方程求解、積分方程求解、特徵值計算和非線性方程組求解等高難度和複雜的數學計算問題,而且在統計物理、核子物理、真空技術、系統科學 、資訊科學 、公用事業、地質、醫學,可靠性及電腦科學等廣泛的領域都得到成功的應用。
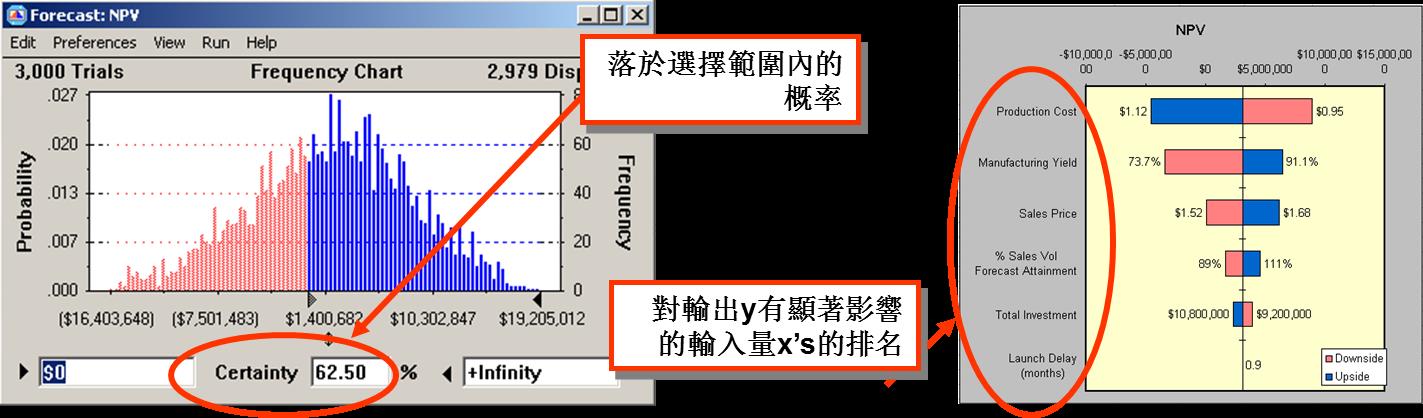
專案管理中蒙特卡羅類比方法的一般步驟
專案管理中蒙特卡羅類比方法的一般步驟是:
1、對每一項活動,輸入最小、最大和最可能估計資料,並為其選擇一種合適的先驗分佈模型;
2、電腦根據上述輸入,利用給定的某種規則,快速實施充分大量的隨機抽樣;
3、對隨機抽樣的資料進行必要的數學計算,求出結果;
4、對求出的結果進行統計學處理,求出最小值、最大值以及數學期望值和單位標準差;
5、根據求出的統計學處理資料,讓電腦自動生成概率分佈曲線和累積概率曲線(通常是基於正態分佈的概率累積S曲線);
6、依據累積概率曲線進行專案風險分析。